This blog posting continues the discussion of how to perform audio analysis on an iPhone. For some background information, please see the previous post – Audio Analysis on an iPhone.
Apple provide a digital signal processing API called vDSP (also known as the Accelerate framework). To quote their website, it provides “ mathematical functions for applications such as speech, sound, audio, and video processing, diagnostic medical imaging, radar signal processing, seismic analysis, and scientific data processing.”
We will be using this to analyse the audio, and extract the frequency information. Initially we will be loading audio from pre-recorded WAV files. Although the ultimate aim is to perform realtime analysis, it’s much easier to develop using pre-recorded files than try to make a bat squeak into a microphone on demand!
The vDSP fourier transform (FFT) functions are a bit tricky to use. For real inputs, they do an in-place FFT, which means the samples in the input buffer are replaced with the output of the FFT. This is possible because for a real FFT of size N, the complex output is symmetrical about N/2. This means the last half of FFT is redundant information, and we can instead use it to store the complex component of the output. For more detailed info, see Apple’s API.
We also want to apply a window function to reduce spectral leakage. We will use a Hamming window.
Out input parameters:
float *samples; // This is filled with samples, loaded from a file int numSamples = 256; // The number of samples
Initialise the FFT:
// Setup the length vDSP_Length log2n = log2f(numSamples); // Calculate the weights array. This is a one-off operation. FFTSetup fftSetup = vDSP_create_fftsetup(log2n, FFT_RADIX2); // For an FFT, numSamples must be a power of 2, i.e. is always even int nOver2 = numSamples/2; // Populate *window with the values for a hamming window function float *window = (float *)malloc(sizeof(float) * numSamples); vDSP_hamm_window(window, numSamples, 0); // Window the samples vDSP_vmul(samples, 1, window, 1, samples, 1, numSamples); // Define complex buffer COMPLEX_SPLIT A; A.realp = (float *) malloc(nOver2*sizeof(float)); A.imagp = (float *) malloc(nOver2*sizeof(float)); // Pack samples: // C(re) -> A[n], C(im) -> A[n+1] vDSP_ctoz((COMPLEX*)samples, 2, &A, 1, numSamples/2);
Run the FFT:
//Perform a forward FFT using fftSetup and A
//Results are returned in A
vDSP_fft_zrip(fftSetup, &A, 1, log2n, FFT_FORWARD);
//Convert COMPLEX_SPLIT A result to magnitudes
float amp[numSamples];
amp[0] = A.realp[0]/(numSamples*2);
for(int i=1; i<numSamples; i++) {
amp[i]=A.realp[i]*A.realp[i]+A.imagp[i]*A.imagp[i];
printf("%f ",amp[i]);
}
We now have the frequency spectrum amplitudes in amp[i] for the first 256 audio samples. If we are sampling at 44kHz, that means we have the spectrum from the first (256/44000) = 0.0058sec of the call. From Nyquist (see previous post), the maximum frequency we can detect is 22kHz, and because our FFT is symmetrical we have 128 output bins. This means each bin width is 22,000/128 = 171Hz. We are using a time expanded bat call here, so the bats original ultrasonic signal (20kHz-100kHz) has been reduced in frequency to a human audible range (0-20kHz).
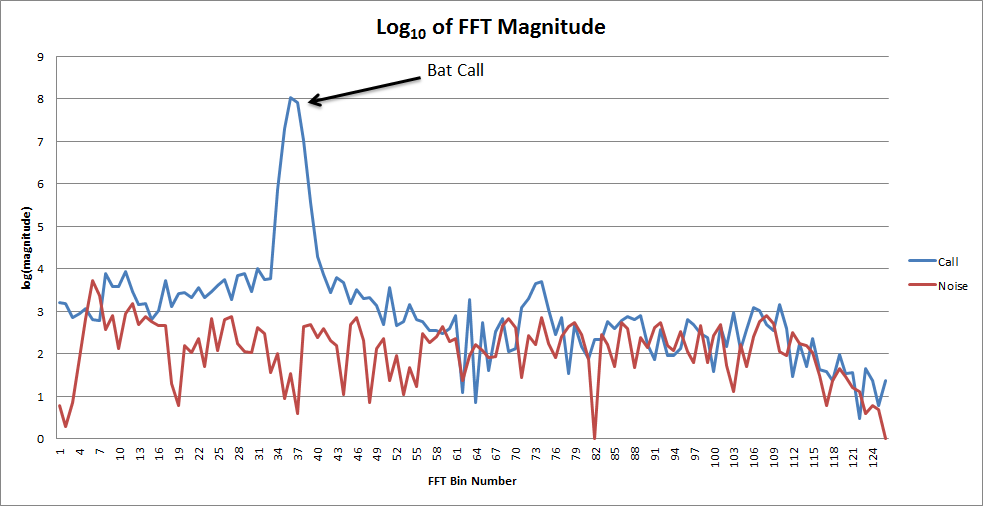
An example of the logarithmic output from the FFT:
We need to detect the start and end of each bat call in our test file. To do this we need to run an FFT on each subsequent set of 256 audio samples, and look for amplitudes in the spectrum ranges of the sounds produced by a bat.
A very rough method to do this would be to maintain a rolling average of the values for certain frequencies (FFT bins), and if a new value is much larger than the average, it’s likely to be a call. There are better ways however, that involve more precise measurement of the background noise, and calculate the signal to noise ratio.
These will be detailed in a later blog post.